I wrote this essay in 1968, and printed it in my magazine In Defense of Variety in 1977. It was republished as a pamphlet in 1987, and reprinted three times with minor changes. The subject is a surprisingly simple but powerful way of making votes express the wishes of the voters. It was conceived by others about the same time, and has been named approval voting. See the Postscript for more on the history of the idea.

For details on the printed pamphlet (which looks better than the web page can!) click here.
For a comparison of Approval Voting with the “Alternative Vote”, click here.

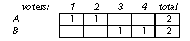
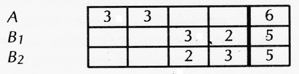
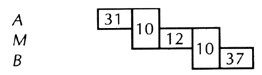
The Arithmetic of Voting

One person, one vote.*

[*footnote: “One man shall have one vote”—John Cartwright, People’s Barrier Against Undue Influence, 1780.]

But one of the consequences of this sacred rule is that the more good options there are (candidates, parties, or measures) the weaker each becomes, and the weaker they become collectively.

Let us suppose that there are two political sides, A and B. If there is one candidate on each side, and if the one-person-one-vote rule applies, perfect justice prevails. That is to say, the division of the vote corresponds exactly to the wishes of the people. If, for instance, the people are exactly divided between A and B (as is unlikely but possible), then the result is a draw, which is awkward but just. For justice in an election means that the division of the votes comes out proportional to the divisions among the voters.

But what if another candidate enters on side B? Philosophically we might think that this ought to strengthen that side. But of course it does just the opposite. If, as before, 50 percent of the people are for A and 50 percent for B, then the two B candidates will now divide 50 percent of the vote between them. They will get perhaps 25 percent each; at any rate, each will get less than 50 percent; and so A will win, not because there are more voters on that side, but because there are more candidates on the other side. If a third candidate enters on side B, the average vote received by the candidates will be divided by three, and so on.

Another way of putting it is that if there are two candidates altogether A needs over half the votes to win; if there are 3, he needs over 1/3; if 4, only 1/4; and so on.

Let us tabulate the situation in a simplified form, imagining that there are four voters, and two “sides,” and the voters are evenly divided between the sides. With one candidate on each side, the result is:

With one side split:

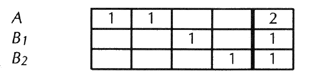
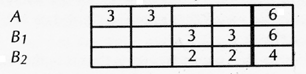
Or the split may be of this kind:

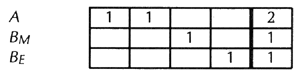
—where the notations “M” and “E” mean “moderate” and “extreme.”

Originally I drafted these ideas in February of 1968. At that time A could be imagined to be Nixon, BM Johnson, and BE King, or McCarthy, or the Peace and Freedom Party; or, conversely, A could be Johnson, BM Nixon, and BE Wallace. That situation has long since passed, but it might be less invidious to think in some such terms than to suggest contemporary equivalents.

I do not apologize for infusing the idea of “good” and “bad” sides into such a discussion. Of course there is never a side that is the good one in everybody’s view, and so it is utterly non-objective to identify one side as the good one. In any specific election, however, and in the minds of individual voters, the sides are good and bad in varying degrees. The very institution of elections assumes this, for it asks the voters to identify the side they consider the good one. From a general point of view, the purpose of elections is the lofty and impartial one of seeing that the majority wishes of the people are respected; but from most individual points of view the far more vitally felt aim is to see that the Republicans (or Socialists, or Christian Democrats . . .) get into power. And neither purpose is truly served by the rule of one-man-one-vote.

The whole thing can be stated in a dispassionate way, without reference to “good” or to “sides”: if, out of three or more candidates, two are similar, and even if a majority of voters prefers either one of these, yet the votes of that majority are split between them, with the result that another candidate is likely to win, though not wanted by the majority.

The primary reason why this seems wrong is that it makes the result of the vote depend more on the distribution of the candidates than on the distribution of the voters’ wishes. Secondly, it is the opposite of the way it should be in that candidates ought to be encouraged, not discouraged, from adding their names to the competition; each new candidate may be an improvement on the others; at any rate the voters have a wider choice, and the statistical chance of electing a good candidate is higher.

Thirdly, you have only to think of the dilemma you are placed in if you happen to be one of the voters supporting side B, especially BE, and especially if it is a relatively small splinter. If there had been only two candidates, you would have voted for the one you considered better. To them is added another whom you consider better still, but he has less chance to win. If you do vote for him, you have in effect given your vote to the candidate you consider worst. On the other hand you feel that if you and others like you do not vote for the one you believe in, his cause will never have a chance to grow.

All this is well known. It is “a fact of political life”; it is “the voter’s dilemma.” Heads are shaken over it at almost every election. It is used: there are many instances in which one side has encouraged extra candidates to run on the other side, even “planted” them there, in order to divide that side. Or, conversely, a side “undivides”: Labour and the Liberal Democrats make a pact not to run against each other in certain constituencies, so that they each will have more chance of beating the Conservatives; this is called “tactical voting.” Because it is known and exploited, do we have to accept it?

First solution that doesn’t work

Let each voter cast as many votes as there are candidates.

The result then might be like this:

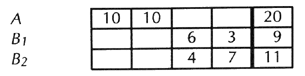
That is, it would be essentially the same as before. Voters on the side where there is only one candidate would give all their votes to him; those on the side where there is more than one candidate either would divide their votes, or would divide among themselves, some giving all their votes to one candidate on the side and some to another. This is in effect the one-vote system still, except that your one vote may be divided into fractions of a vote.

Second solution that doesn’t work

Let each voter put the candidates, or as many as he wishes to vote for, in order—1st, 2nd, 3rd. Count his first choice as 3 votes, his 2nd as 2, his 3rd as 1.

Result:

Again, the average of the votes for each candidate on the divided side is inevitably lower than the number of votes for the one candidate on the undivided side.

One of the candidates on the divided side could come out level with the candidate on the undivided side, but only if every voter on his side puts him first:

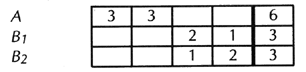
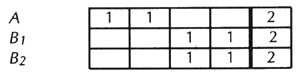
Third solution that doesn’t work

Let each voter cast as many votes as he likes, up to some predetermined number, such as 10.

This is really just a variant of the first solution, with the number of votes per voter changed. And so the result will be essentially the same:

These first three solutions are really all weighted-vote systems. In the first and third, the voter determines the various kinds of weight he can give to his own votes; in the second, it is determined in advance for him.

Solution that works

Let each voter cast as many single votes as he likes, provided they are all for different candidates.

Result:

This is stalemate, as it should be in the hypothetical situation where the two “sides” are exactly equal. If, as would happen in reality, one of the two sides has slightly more adherents than the other, then one of the candidates on that side will win. The “splitting” of side B between two (or more) candidates has not lowered the potential number of votes for each of those candidates.

This system can be seen as negative voting. Giving one vote each to every candidate you don’t mind electing is equivalent to voting, instead, against everyone you do not want to see in office. Thus in our example the two voters who voted for both B candidates could be said to have voted against A.

With three candidates, you could cast up to three votes; but casting all three would have the same effect as not voting at all. As this shows, a voter casting more than one vote does not exercise more power. Indeed, if there is just one candidate you want to help, you can do so most powerfully by casting only one vote.

Thus far I have been simplifying to the extreme. What kind of difference will it make when, instead of imagining that there are two clear-cut “sides,” we deal with the possibility that there is overlap between them? Or when the numbers of their supporters, instead of being small and equal, are large and irregular?

Here is a somewhat more flexible kind of tabulation, which will allow us to play with examples of these more real and complicated situations:

In this particular situation, 40% of the electorate supports only A, 30% only the moderate B, and 5% only the extreme B. 10% are the “floating” or potential “cross-over” voters, the ones who don’t mind voting for either Democrat or Republican (say) but want to keep the extremists out. 15% are the ones who would perhaps prefer the extreme B, but may realistically have to support the moderate B if they want to keep A out.

The result under the present system can vary widely, because of what these latter two groups may choose to do. The 15% group may opt for either BM or BE, depending on how they decide to resolve the rather agonizing dilemma we referred to already. This is really a tactical decision; it is not an ideological one. And really therefore it is not the sort of thing that voters should be asked to decide: they are supposed to be voting in order to express their preference; they should not be asked to make calculations of expediency which should be part of the job of the politicians themselves or of political analysts. The 10% group may opt for either A or BM; they are not in a dilemma, or at least not of the same tactical kind—they opt one way or the other because of the latest speeches of the candidates, or trends of the economy, and these are indeed matters that should concern the voter.

In practice, of course, the 10% group will split, in any one of an infinity of different proportions; so may the 15% group; so there are not five possible results but an infinity. This kind of unpredictability in results is not a sign of some kind of richness in the present system, but is a sign of failure in it. We must distinguish between two kinds of variation: variation in the underlying numbers of people who feel in sundry ways; and variations in what may result, given one pattern of those numbers. Here we are imagining that, like God, we know the underlying pattern: 40% feel in favor of A only, and so on. Given this pattern, there should ideally be one result, expressing the wishes of the people; not a variety of possible results, expressing merely the fact that some people are forced into a dilemma. Under the proposed system, such people can vote for both the candidate they really want and the next-best candidate who has a better chance of winning. There is (given our still rather simple “underlying pattern of wishes”) one possible result. And from a count of the actual votes cast for A only, for A+BM, and so on, it would actually be possible to reconstruct our table that sets out the “underlying pattern of wishes.” No longer will only God know it!

The numbers of votes the three candidates get really represent the numbers of people who are not against them. That is why they add up to more than 100%: many voters are not-against more than one candidate. In the particular example, BM is the candidate with the largest number of people for, or rather not against, him; so under the proposed system he wins. Under the present system he could win but is more likely (given the structure of our numbers) to lose to A.

BE is the “extreme” candidate with the smallest support. In the present system he may end up with only his hard-core supporters voting for him (5%). This is not really fair: he has more sympathizers than that; but with so little actual help from their sympathy his cause may wither away. His votes can range up to 20%, the actual amount of his sympathizers, but only as an unlikely upper limit. In the proposed system, however, he receives 20% of votes. He still comes third, but the amount of support he has is actually expressed in votes, and he can proceed to build from there.

Another type of political situation can be represented like this:

Here M (a notation that evolves easily out of our BM) is a small party of the middle. (The parties might be thought of as the British Labour, Liberal, and Conservative.) In the traditional system M can receive up to 32% of the vote, but is likely to receive little more than 12%, since its sympathizers in the two 10% groups fear that they will be throwing away their votes unless they give them to the large parties. A can receive from 31% to 41% and B from 37% to 47%, so it is uncertain which of them will win, the uncertainty depending on which way the 10% groups resolve their dilemmas. The traditional system is therefore unfair to the middle in a situation like this. In the proposed system, A gets 41%, M 32%, B 47%; B wins, as it should, and M gets a proportion of votes that shows the extent of its support fairly.

You are welcome to think of other situations and analyze them by means of the same sort of diagram; perhaps more insights will emerge about the weaknesses or strengths of the suggested system.

There are two quite serious criticisms that you may already have noticed; but if you have noticed both of them you may also notice that they are approximately opposite to each other.

The first is that the system favors parties of the middle. The probability that a middle-of-the-road party will win is increased over that probability in the present system, because, in the proposed system, people from the areas both to right and to left of it can more readily vote for it: while still preferring, and still voting for, a party on the flank, they can also vote for the party in the middle without fearing that they are damaging their own flank party.

The other criticism is that the proposed system favors parties of the extremes! Actually this applies to any small, relatively unsuccessful, or new party. Instead of giving it only the small number of votes representing its hard-core support—the people who insist on voting for it even while knowing that it has no chance of winning—the system will tend to give it the larger number of votes representing the people who don’t mind it, or prefer it, because they can vote for it without detracting from their support of the larger next-best party.

Probably no decision about an electoral system is without its effect on the outcome—no change in voter-registration procedures, district boundaries, ballot apparatus, or any other matter of method, is pure of effects on the actual fortunes of Republicans, Tories, or whoever is concerned. A change in method whose possible effects are to put into office parties that the fewest people object to, and to show the true extent of the support for all parties including the small ones, seems as benevolent as any.

This form of voting is the second simplest after one-person-one-vote. It is time to give this costless reform a conspicuous trial.

Postscript: the history of this idea

I sketched this essay in Manchester (England) around 1962, including the diagrams as shown here; wrote it fully in February 1968, passing it to friends in Los Angeles for comment. Eventually I printed it in my magazine In Defense of Variety (July-August 1977).

Unknown to me, the idea was put forward by several others about the same time: John Kellett and Kenneth Mott (“Presidential Primaries: Measuring Popular Choice,” in Polity, Summer 1977); Robert J. Weber (“Comparison of Voting Systems,” mimeographed, 1977); Steven J. Brams and Peter C. Fishburn (“Approval Voting,” American Political Science Review, September 1978); and Richard A. Morin (Structural Reform: Ballots, New York, Vantage Press, 1980).

The expression “approval voting” was coined by Weber. I had touched on this aspect (“Giving one vote each to every candidate you don’t mind electing  . . . ,” “The votes  . . . really represent the numbers of people who are not against them”) but I had forgotten to think of a handy term. “Acceptance” might do as well as “approval.”

The only discussions of voting-systems I had seen were in the June 1976 Scientific American and subsequent correspondence. The solutions mentioned seemed unrealistically elaborate—requiring after-the-vote analysis by computers—and did not include approval voting. This was the provocation that made me publish my article. But in the October 1980 issue of the same magazine approval voting was mentioned by Martin Gardner in his “Mathematical Games” feature, and with his help I got into correspondence with Brams.

Brams has done most of the publishing about and campaigning for the idea since. His and Fishburn’s book Approval Voting appeared in 1983; it contains bibliography and history, an informal description of the advantages of the proposal including several not mentioned by me, eight chapters of technical analysis, and a “Bill to Enact Approval Voting in New York State.”

Approval voting was actually used in Massachusetts in the eighteenth century. Members of the United Nations Security Council are allowed to vote for more than one candidate for Secretary General. In a typical election for 12 members of a board, there are, say, 19 nominees and the instructions are to “Vote for up to 12”; and it is not clear that anything would be lost by letting voters vote for any number.

Copyright © 2004 by Guy Ottewell
 July 1987; reprinted with slight improvements Sep. 1999, Jan. 2001, Apr. 2004

A step further than approval voting is range voting, in which (1) voters give each candidate a number between, say, 0 and 100, or 0 and 10; (2) they can opt to give no opinion on a candidate, without affecting that candidate's chances. Feature 1 makes the system more sensitive than approval voting but more complicated, and I fear that it brings back the "voter's dilemma". I think that feature 2 is a definite solution to a need. Range voting is very fully described by its proponent Warren Smith at http://rangevoting.org